Teoria gier w zarządzaniu
-

- Jarosław Badurek,
- 24.07.2020, godz. 08:02
Gry komputerowe, które niedawno traktowano jako kolejną zabawkę, dziś są nie tylko wielomiliardowym biznesem, ale w połączeniu z teorią gier zyskują na znaczeniu jako platforma do rozwoju oprogramowania gospodarczego czy badań nad sztuczną inteligencją.

Teoria gier jest stosunkowo nowym działem matematyki, badającym znajdowanie optimów w sytuacjach konfliktowych. To mogą być sprzeczności interesów przedsiębiorstw na rynku czy pośród członków zespołu projektowego. Obszar, który wyłonił się z zainteresowania grami hazardowymi (były także istotne dla rozwoju statystyki) w pierwszej połowie minionego stulecia, doczekał się solidnych podstaw naukowych, a w drugiej został wzbogacony o implementacje informatyczne, np. gry symulacyjne w modelowaniu gospodarczym.
Dodatkowym sprzężeniem interdyscyplinarnym, jakie warto wymienić, jest wpływ gier komputerowych na rozwój technologii informatycznych, w szczególności wysokowydajnego sprzętu.
Zobacz również:
Dość powiedzieć, że aktualne prognozy magazynu „Forbes” umieszczają gry komputerowe wśród trzech najważniejszych trendów technologicznych obok sieci 5G i autonomicznego transportu wspomaganego sztuczną inteligencją.
Z kolei samą teorię gier można też postrzegać jako fragment krajobrazu modeli zajmujących się zarządzaniem systemami złożonymi CEP (complex event processing – złożone przetwarzanie zdarzeń). Problemy, z jakimi stykamy się we współczesnej gospodarce, można by w kategoriach organizacyjno-informacyjnych sklasyfikować właśnie jako zarządzanie systemami złożonymi, a więc takimi, które składają się z bardzo dużej ilości obiektów i wielkiej ilości relacji między nimi. Niemal na zasadzie: wszystko jest połączone ze wszystkim, tj. zgodnie z wszechobecnym w społeczeństwie i przedsiębiorstwie informacyjnym paradygmatem sieciowości.
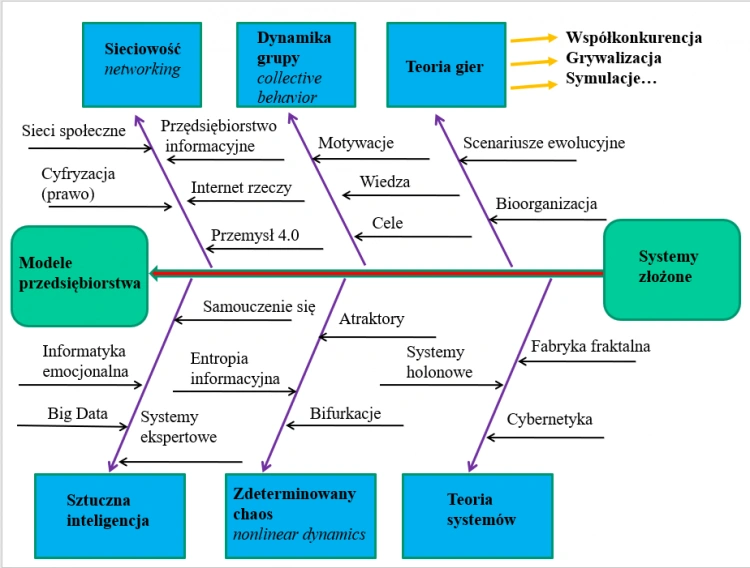
Teoria gier w modelowaniu systemów złożonych przedsiębiorstwa
Wspomniany wymiar organizacyjny oznacza w istocie zarządzanie systemem informacyjnym wspomaganym informatycznie. Z jednej strony mamy w takim kompleksie ludzi, z drugiej strony technologie – komputery, ale także inną infrastrukturę logistyczną czy maszyny produkcyjne. Dostrzegamy, że złożoność współczesnych systemów gospodarczych prowadzi do przetwarzania wielkich i coraz większych ilości danych, ale przyrost ich jakości jest znacznie mniejszy. Wiemy bowiem, że ilość danych informatycznych na świecie rośnie wykładniczo.
W roku 2024 możemy się spodziewać ok. 149 zettabajtów w skali planetarnej, wobec ok. 59 obecnie. Przypomnijmy, że 1 ZB = 1021 B, a na wszelki wypadek warto też zapamiętać następną w kolejności jednostkę, 1 YB (jottabajt, 1024 B).
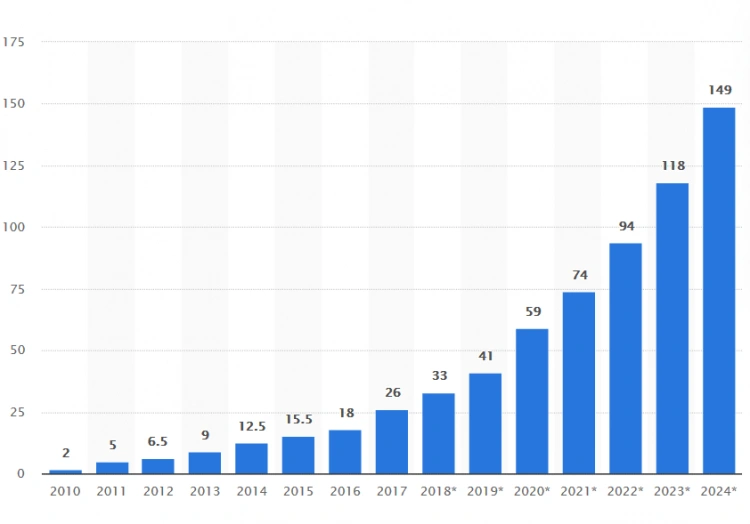
Światowa wielkość infosfery w zetabajtach (prognoza, źródło: statista.com, maj 2020)
Modele systemów złożonych, w skład których wchodzi teoria gier, łączone są z klasycznymi już metodykami zarządzania procesami biznesowymi. Teorię gier znajdziemy zarówno w zarządzaniu Przemysłem 4.0, a więc internetem rzeczy i systemami cyberfizycznymi CPS, jak i w sferze Big Data. Celem tej ostatniej technologii jest nadanie procesom eksplozji danych właśnie wymiaru jakościowego. Stąd Big Data może być definiowane w ramach modelu 4V jako duże ilości danych (Volume) o znacznej różnorodności (Variety) i zmienności (Velocity) prowadzące do uzyskania nowej wartości (Value) decyzyjnej w odniesieniu do optymalizowanych procesów (biznesowych). Zilustrujmy te zależności przykładami z praktyki komputerowo wspomaganego zarządzania.
Gra w inteligencję
Rozwój gier komputerowych, które coraz lepiej symulują rzeczywistość, w połączeniu z teorią gier zaowocował także przekształceniem niektórych z nich w systemy o bezpośrednich zastosowaniach biznesowych. Przykładowo problem planowania zakupów w przedsiębiorstwie może być postrzegany jako rodzaj rozgrywki, której celem jest optymalizacja poziomu zasobów i ich wykorzystania. Planista ma tu do wykonania zadanie podobne to tego, jakie stoi przed graczem, który również musi przewidywać swoje działania i robi to na różnych poziomach: strategicznym (główny cel gry), taktycznym (cele cząstkowe) i operacyjnym (akcje w czasie rzeczywistym).
Inteligencja programów informatyki gospodarczej, np. systemów ERP, jest wysoka na poziomie algorytmicznych heurystyk. Ale prezentowane są one w sposób właśnie maszynowy, a więc mniej „ludzki” – za pomocą szeregów liczb, tabel czy w najlepszym przypadku grafiki, i to z reguły tylko statycznej. W samej teorii gier modele rzeczywistości również ograniczają się głównie do układów równań, co może stanowić jedynie punkt wyjścia dla pełniejszego odwzorowania dynamicznych procesów przedsiębiorstwa.
Tymczasem gry komputerowe śmiało i efektywnie operują generatorami dialogów, włącznie z syntezą mowy, zmierzając w trudniejszym kierunku jej analizy, co jest cennym źródłem doświadczeń dla szerszego korzystania z interfejsu głosowego i przetwarzania języka naturalnego już w zastosowaniach gospodarczych.
Grafika gier komputerowych jest dynamiczna, a jej celem jest osiągnięcie jak największej wierności w odwzorowywaniu obiektów świata rzeczywistego (wirtualna rzeczywistość).
Jednocześnie podmioty występujące w grze uwzględniają w dużym stopniu psychologię zachowań ludzkich. Dotyczy to zarówno czasu reakcji komputera – ten mógłby być przecież nienaturalnie szybki – jak i jego postępowania. Program brydżowy nie może korzystać w grze z pełnej wiedzy o rozkładzie kart na wszystkich rękach, mimo formalnego posiadania tych danych. Powoduje to, że inteligencja gier komputerowych jest bardziej naturalna, bo obarczona pewnymi elementami niedoskonałości.
Oprogramowanie o takich cechach może w pewnych sytuacjach lepiej symulować rzeczywiste procesy gospodarcze niż formalnie sprawniejszy i doskonalszy algorytm. To właśnie połączenie matematycznej teorii gier oraz jej rozrywkowych zastosowań stało się genezą nowej dziedziny informatyki gospodarczej o wielkich perspektywach – uczuciowej (affective computing).
Gry decyzyjne
W każdej dziedzinie sama teoria to za mało, potrzebne jest jej połączenie z praktyką. Tak też jest w algorytmice, która jest przecież częścią wszystkich obszarów informatyki a więc również tu omawianych. Przykładowo: czy mając w naszej firmie 100 ciężarówek, które muszą rozwieźć towar do 100 klientów w 100 miastach, jesteśmy w stanie określić ich trasy przejazdu, gwarantujące minimalne koszty transportowe? Podstawy teorii zarządzania, które obejmują badania operacyjne, natychmiast nasuwają tu skojarzenia ze znanym „problemem komiwojażera”. Zagadnienie opracowano matematycznie ok. 100 lat temu, a badano już wiek wcześniej.
Pomińmy dalej szereg wersji tego klasycznego problemu (np. symetrycznych, asymetrycznych), koncentrując się właśnie na praktycznej stronie „gry” logistycznej. Dla uproszczenia, zajmijmy się tylko jednym pojazdem startującym z ustalonego miasta. Nasza ciężarówka ma do wyboru 99!, czyli ok. 10155 możliwości. Według listy najszybszych komputerów świata Top500.org, całkowita moc 500 pierwszych razem wynosi 1,65 egzaflopsa (1018 operacji zmiennoprzecinkowych na sekundę). Zaokrąglijmy liczbę 1,65 solidnie w górę do 10 i załóżmy, że istnieje w kosmosie nawet milion takich cywilizacji jak nasza, a więc dysponujemy mocą 10 milionów EF czyli 1025 flopsów.
Nawet gdyby te komputery pracowały milion lat, to i tak nie pomogłyby naszej firmie w rozwiązaniu problemu przy założeniu, że chcielibyśmy przeliczyć po kolei wszystkie możliwe kombinacje tras.
Doba to tylko niecałe 105 sekund, w roku nie ma ich zatem nawet 108, czyli w ciągu miliona lat jest mniej niż 1014. Daje to 1039 operacji dla naszego supersuperkomputera. Jakkolwiek liczyć, brakuje jeszcze grubo ponad 100 zer w potędze wyjściowej liczby kombinacji.
Przyjmując, że wszechświat składa się z 1080–1090 atomów, widzimy, że nawet gdyby każda jego cząstka stała się takim superkomputerem, to i tak nie uzyskamy wyniku, choćby liczyć je od wielkiego wybuchu ok. 15 mld lat temu. Dodajmy, że współtwórca teorii informacji, Claude Shannon, oszacował liczbę kombinacji gry w szachy na 10120 (tzw. liczba Shannona, obecnie szacuje się złożoność drzewa tej gry na 10123).
Dotąd mówiliśmy tylko o jednym pojeździe, a już nam się (wszech)świat kończy. Co dalej? Przecież problem jest teoretycznie znacznie bardziej złożony, i to o potężne rzędy wielkości. Ciężarówki mogą mieć przecież różne parametry załadunkowe – to kolejne utrudnienie. Transportowane ładunki musimy także powiązać z optymalnym komisjonowaniem (zlecenie klienta i zlecenie transportowe nie muszą być tożsame). Odrębne kwestie to: zarządzanie kierowcami, dynamiczne delegowanie transportu do innych firm, zbiorcze punkty transportowe, ładunki zwrotne czy okienka dostaw definiowane przez klienta. Każda kolejna grupa parametrów dodatkowo potęguje złożoność i tak bardzo trudnego problemu.
Co robi zatem nasz dyspozytor w praktyce? Rozbudowuje układy równań liniowych? Nie, raczej je ignoruje. Okazuje się, że człowiek z reguły unika strategii polegających na mozolnym rozważaniu wszelkich możliwych wariantów decyzyjnych. Wystarczy oprzeć się na doświadczeniu i zdrowym rozsądku, wybierając niejako intuicyjnie rozwiązanie, które wydaje się najlepsze, jednocześnie z góry odrzucając większość wariantów. Te selektywne zdolności ludzkiego umysłu w algorytmice odpowiadają heurystykom i prowadzą do rozwiązań akceptowalnych w praktyce, mimo że nie są one w 100% teoretycznym optimum.
Jednocześnie udowodniono, że niektóre heurystyki prowadzą do rozwiązań, które można uznać za dokładne nawet dla dużej ilości danych (np. program Concorde i heurystyki Wiliama Cooka o odchyleniu mniejszym niż 1% od optimum TSP). Dodajmy, że złożoność czasowa różnych heurystyk TSP jest proporcjonalna do n2 (n – liczba węzłów), dla n = 100 mamy tylko 104, to naprawdę niewiele, nawet jeśli elektronicznym graczem jest zwykły pecet.
| Przykłady zastosowań teorii gier w przedsiębiorstwie | |
|---|---|
| Grywalizacja, gamifikacja | Wykorzystywanie schematów wypracowanych przez gry (np. World of Warcraft) w działaniach grupowych (np. zdania, poziomy, nagrody, kolekcjonowanie) |
| Konkuperacja, współkonkurencja (konkurencyjna kooperacja) | Modele korzystające z centralnej w teorii gier, równowagi Nasha |
| Gry symulacyjne | Testowanie mechanizmów cyberbezpieczeństwa (dynamiczne scenariusze cyberataku) |
| Ewolucyjna teoria gier | Paradygmat bioorganizacyjny w gospodarce (przedsiębiorstwo jako żywy organizm) |
| Modele sieci wartości | Wyznaczanie strategii biznesowych przy użyciu dynamicznych map relacji partnerskich |
| Planowanie kolejności zleceń wytwórczych | Systemy dialogowe typu Graphic Planboard |

