60 lat temu inżynierom z firmy Texas Instruments (USA) udało się skonstruować pierwszy układ scalony. Konsekwencją tego wynalazku było pojawienie się na rynku serii maszyn cyfrowych IBM 360. W tym samym czasie pomnikowa postać mikroelektroniki Gordon Moore, założyciel firmy Intel. formułuje swoją słynną prognozę, przewidującą podwajanie się gęstości upakowania układów scalonych co ok. dwóch lat. Reguła nie pretenduje do miana ściśle naukowego prawa, a jest jedynie ogólną hipotezą empiryczną (okres podwojenia waha się od 18 do 24 miesięcy), sprawdzającą się jednak od lat w praktyce.

Dla scalonych tranzystorów upakowanych w „kostce” mikroprocesorowej istotnym parametrem jest szerokość ścieżki, czyli podstawowa wielkość tych mikrostruktur. Formalnie chodzi tu o minimalną długość kanału tranzystora, nazywaną wymiarem charakterystycznym zwłaszcza dla technologii CMOS (Complementary Metal-Oxide Semiconductor). Gęstość upakowania „scalaków“ wiąże się z tzw. węzłami technologicznymi, czyli skokami technologicznymi opisywanymi właśnie rozmiarem najmniejszej możliwej struktury fotolitograficznej.

Zobacz również:

• Kwanty od OVHCloud dla edukacji
• Microsoft i Quantinuum twierdzą, że otworzyły nowy rozdział w rozwoju komputerów kwantowych

Istotne zasługi w prognozowaniu i szacowaniu kosztów przechodzenia do kolejnych technologii ma International Technology Roadmap for Semiconductors, gremium sponsorowane przez światowych producentów półprzewodników. W tabeli „Wybrane węzły technologiczne półprzewodników” prezentujemy wybrane przykłady omawianych technologii. Ich limity, czyli minimalna szerokość umownie rozumianej ścieżki, są ciągle obniżane.

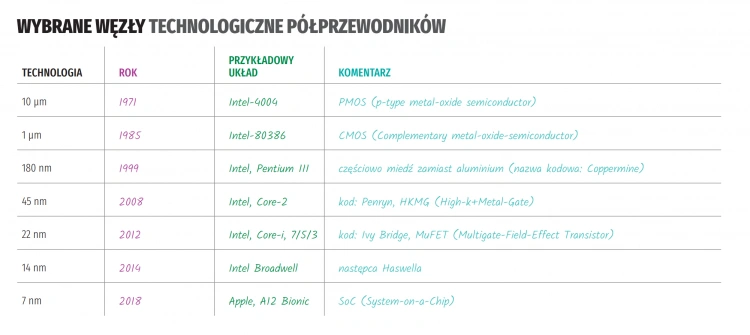
Obecnie przyjmuje się, że w kolejnej dekadzie zostanie osiągnięta szerokość na poziomie 2–3 nm, z uwagi na granice stabilności mechaniki kwantowej. Również i z tego powodu interesujące jest poszukiwanie alternatyw dla obecnej informatyki półprzewodnikowej. Jedną z nich są komputery kwantowe.

Dla zrozumienia, w jaki sposób takie urządzenia mogą działać, powinniśmy przypomnieć sobie kilka informacji z kursu fizyki. Są to m.in. eksperymenty z naświetlaniem szczelin, korespondujące z falowo-cząsteczkowym opisem światła (Young, XIX w.), oraz niekonwencjonalne tłumaczenie ww. dualizmu modelem równoległych wszechświatów (Everett, lata 30. XX w.). Do tego dochodzi jeszcze idea komputera kwantowego liczącego w wielu wszechświatach i udostępniającego wyniki w „naszym“ (Feynmann, lata 80. XX w.) i oddziaływania splątane wykorzystujące fenomen superpozycji cząstek.

Zatrzymajmy się na chwilę przy ostatnim zjawisku. Jego plastyczne wyjaśnienie znajdziemy w pracy współczesnego badacza, prof. Antona Zeilingera „Dance of the photons“, dostępnej także w polskim tłumaczeniu – „Od splątania cząstek do kwantowej teleportacji”. W książce znajdziemy rysunek i opis piruetu łyżwiarza, który znajduje się właśnie w takim wielostanie, stan ustalony uzyskamy, gdy sportowiec się zatrzyma w określonej pozycji. Wiemy, że klasyczny komputer operuje bitami przyjmującymi dwa stany: 0 lub 1. Komputer kwantowy operuje bitami kwantowymi, czyli kubitami (quantum bit, qubit, qbit). Kubit może mieć wartość 1 w jednym wszechświecie i być jednocześnie zerem w innym. Fajnie! Czy to oznacza, że dwa kubity to cztery wartości, a trzy to 8? Dokładnie tak. Ktoś wzruszy tu ramionami: ależ to znana formuła 2N. Faktycznie, z jednym istotnym dodatkiem: stany te osiągane są jednocześnie.

Uzupełnijmy to jeszcze twierdzeniem miło brzmiącym dla ucha każdego matematyka: pamięć komputera kwantowego można interpretować jako 2N-wymiarową przestrzeń Hilberta. Tyle teorii, ale przecież te kubity muszą mieć jakąś materialną reprezentację. Czy nasz q-komputer to labirynt płytek z fantazyjnie powycinanymi szczelinami, przez które hulają fotony? Raczej powinniśmy sobie go wyobrazić w postaci sieci punktów kwantowych (ang. quantum dot, qudot) reprezentujących kubity. Taki punkt może być tzw. pułapką jonową, czyli elektronem uwięzionym w polu elektrycznym.

Komputery kwantowe. Znikający punkt

Jeśli elektron potraktować odpowiednim promieniowaniem laserowym, to będzie zmieniał swoje stany energetyczne. Powiedzmy, że wyższy poziom energetyzcny elektronu traktujemy jako jedynkę, a niższy jako zero. Zmiany częstotliwości światła laserowego powodują „skakanie” elektronu między tymi poziomami. Mamy zatem nasz podstawowy przełącznik do budowy komputera. Ale siła informatyki kwantowej polega także na stosowaniu innej logiki niż w systemach klasycznych. Otóż skrócenie czasu naświetlania elektronu powoduje, że znajdzie się on w stanie „niezdecydowanym", będącym kombinacją dwóch poziomów. Z kolei mając kwantową negację QNOT, możemy realizować bardziej złożone funkcje logiczne, łącząc kubity w pary itd.

Niestety, w tym momencie napotykamy poważne bariery praktyczne takich konstrukcji. Po pierwsze, elektron może pozostawać w podwyższonym stanie energetycznym ok. jednej mikrosekundy, jeśli zatem „obliczeniowy” impuls lasera trwa np. jedną nanosekundę, czyli 1000 razy krócej, to widać, że liczba operacji na takim kubicie jest ograniczona, gdyż po tym czasie nasza kwantowa pamięć po prostu straci swoją zawartość.

Ponadto komputer powinien składać się z tysięcy punktów kwantowych, a ich rozmiary są tak małe jak 10 atomów (1 nanometr) – taka technologia w stabilnej i powszechnie dostępnej wersji dziś po prostu nie istnieje. Wreszcie na niewielkiej przestrzeni trzeba by umieścić tysiące małych laserów dla indywidualnego naświetlania punktów kwantowych albo skonstruować laser o wielkiej rozdzielczości częstotliwości – na razie w prakyce nie mamy takich urządzeń.

Komputery kwantowe. Gdzie jesteśmy dziś?

To istotne pytanie dla prognozowania informatycznych technologii kwantowych. Od odpowiedzi na nie zależy ocena wiarygodności zapowiedzi różnych firm typu: „za kilka lat będzimy mieli komputery kwantowe“. Czy obecne rozwiązania kwantowe to epoka lat 40. ubiegłego stulecia, kiedy istniały technologie IT oparte na przekaźnikach (np. komputer Z3, 1941 r.) lub lampowe (np. ENIAC, 1946 r.)? Porównywanie jest trudne, bo przejście do informatyki kwantowej będzie skokiem większym niż podczas powstawania kolejnych generacji sprzętowych (po lampach – tranzystorowe, a następnie scalone, o coraz większej gęstości upakowania, aż do mikroprocesorów). W informatyce kwantowej zmienią się nie tylko sfera hardware’owa, ale podstawy algorytmiki. Być może trzeba będzie nawet redefiniować samo pojęcie algorytmu. Przypomnijmy, że obecnie wiąże się ono z zasadą deterministyczności: komputerowy program daje zawsze ten sam wynik dla tych samych danych wejściowych, łącznie z przetwarzanymi parametrami wewnątrzprogramowymi.

Tymczasem komputer kwantowy ma korzystać z superpozycyjnej logiki splątanej w miejsce klasycznej, binarnej. Jeślibyśmy zatem pozostali przy deterministycznym paradygmacie algorytmiki, to mielibyśmy do czynienia z paradoksem: uzyskiwanie ustalonych, trwałych wyników działania software’u za pomocą nieustalonych wielostanów sprzętowych. Tymczasem do tej pory nie znamy innej informatyki niż deterministyczna. Nie zmienia tego faktu nawet stosowanie generatorów liczb losowych, bo w istocie są one tylko pseudolosowe, a więc także generowane na przewidywalnej drodze algorytmicznej.

Komputery kwantowe. Miliony kubitów poszukiwane

Wydaje się, że poziom rozwoju współczesnej informatyki kwantowej odpowiada raczej latom 30. XX w. w informatyce klasycznej. Powstawały wówczas istotne prace teoretyczne (von Neuman, Atanasoff, Shannon) oraz analizator różnicowy ogólnego przeznaczenia – jedna z pierwszych zaawansowanych maszyn liczących w praktycznym użyciu. Tamta informatyka miała charakter analogowy, analizatory, o których mowa, były jednak progiem dla powstania współczesnej informatyki dyskretnej (cyfrowej).

Eksperymenty informatyki kwantowej nie wychodzą jak dotąd poza pojedyncze zestawy kubitowe i nie mamy jeszcze powszechnie dostępnej technologii ich wytwarzania. Zostawmy w tym miejscu niekończące się dyskusje na temat tego, co już jest kwantowym komputerem, a co jeszcze nie. Za charakterystyczne przyjmijmy doniesienie IBM z początków bieżącego roku o udostępnieniu zestawu 20-kubitowego. Ta liczba pokrywa się z publikowanymi wynikami laboratoryjnych eksperymentów wykorzystujących wymienioną pułapkę jonową.

Inną technologią są spinkubity wykorzystujące właśnie zjawisko elektronowego spinu. Korzystają one także ze znanych technologii półprzewodnikowych (stabilność!) w wariancie tzw. zerowymiarowym, co prowadzi do uzyskiwania wspomnianych wcześniej „kropek kwantowych“. W tym kontekście mówi się także o tzw. stylizowanych atomach. Efekt praktyczny jest tu skromniejszy: jak dotąd nie uzyskano kontrolowanych stanów dla więcej niż dwóch spinkubitów.

W kubitowym świecie znajdziemy także fenomen, który od zawsze próbuje się wykorzystać w informatyce (jak dotąd z niewielkim skutkiem): nadprzewodnictwo. W tym celu sięga się po urządzenia SQUID (Superconducting Quantum Interference Device), czyli niezwykle precyzyjne mierniki pola magnetycznego. Efekt: do 10 stabilnych kubitów. Pojedyczne pokazy dochodzą nawet do 72 kubitów, bez gwarancji stabilności. Zgrubnie można przyjąć, że algorymiczne efekty postklasyczne pojawią sie dopiero dla 100 kubitów.

Teoretycznie, do rekordowych wyników można by zaliczyć osiągnięcia kanadyjskiej firmy D-Wave, „w porywach“ dochodzącej do ok. 2000 kubitów. Również i w takich przypadkach, co typowe dla sfery informatyki kwantowej, mamy do czynienia tylko z bardzo specjalistycznymi algorytmami, nie ma tu mowy o zastosowaniach uniwersalnych (klasyk QI to algorytm sortujący Shore’a, 1996r.). Dodajmy przy tym, że zestaw kubitowy „nie pojedzie sam”.

Dla zagwarantowania stabilności i szybkości bijącej parametry krzemu niezbędna jest armia kubitów kontrolnych. Już tylko dla setki kubitów potrzeba nawet miliona „kontrolerów”. Kwantowy komputer takich rozmiarów to dziś ciągle bardziej fiction niż science.